Radian 라디안(호도법)이란?
라디안이라는 것은 각도를 수치로 나타내기 위해 나타난 개념임.
그런데 라디안을 왜 쓰냐고 ?
삼각함수의 수학적 응용을 늘리고, 삼각함수에 대한 계산을 편하게 하기 위함.
일단 이유는 그냥 그렇다고 이해만 하고 개념을 이해해보자.
라디안은 (호의 길이 / 반지름)으로 값을 나타낸다.
반지름이 1인 원의 호의 길이가 1인 중심각을 1 라디안이라고 함.
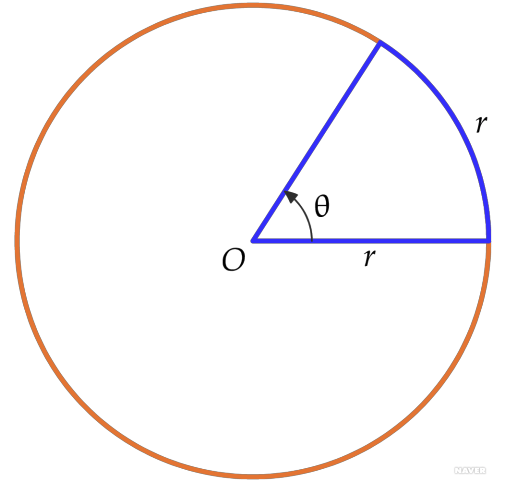
우선 반지름 1, 호의 길이 1 = (호의 길이 / 반지름) → 1 rad 이다.
그러면 반지름 1, 호의 길이 2 = 2 rad.
반지름 1, 호의 길이 3 = 3 rad.
자 그러면 반원의 중심각은 180도이고
반원의 호의 길이는 원의 둘레 공식에 의해 3.14가 된다.
반지름 1, 호의 길이 π = π.
고로 180° = π
180° 의 길이는 π 가 된다.
이렇게 되면 1 radian의 값도 구할 수가 있는데,
1 radian의 디그리 값을 x 로하고 비례식을 써보면
180° : π = x : 1
xπ = 180°
x = 180° / π
x = 57.2958
반대로 1° 의 라디안 값을 구해보면
구하려는 라디안 값을 x로 둬서 비례식을 세우면
180° : π = 1° : x
위 식과 똑같다
x = π / 180°
1° = π / 180° = 0.0175 radian
그래서 우리는 디그리 값과 라디안 값을 변환할 때 위 값을 곱해준다.
디그리 값을 라디안 값으로 바꾸기 위해서 π / 180° 를 곱해주고
라디안 값을 디그리 값으로 바꾸기 위해서 180° / π 를 곱해준다.
삼각함수(sin, cos, tan, acos등등..)를 사용할 때는 삼각함수의 인풋과 아웃풋의 값들이 전부 라디안 값이기에 우리가 디그리 값을 계산한다면 필수적으로 위 값을 곱하여 라디안 값으로 바꿔서 인풋에 넣어줘야 한다.
그리고 삼각함수를 통해 나오는 아웃풋도 라디안 값이기에 디그리 값으로 변환해줘야 각도 계산에 사용이 가능하다.
그런데 이러한 변환식을 유니티에서나 다른 프레임워크, 언어들에서 대부분 Math관련 라이브러리에서 지원을 해주고 있을 것이다.
유니티에서는
Mathf.Rad2Deg
Mathf.Deg2Rad
이러한 함수를 지원하고 있어 해당 함수를 곱해주기만 한다면 변환이 간단하게 가능하다.
사실 그냥 삼각함수를 쓸 땐 저 함수들을 곱해서 사용하자~ 정도로 이해하고 넘겨도 개발하는데 문제는 없을 테지만 정확히 이해하고 사용하느냐 그냥 사용하느냐는 큰 차이가 있다고 생각하기에 복습하는 겸 정리를 해봤다.
'개발이야기' 카테고리의 다른 글
| 디퍼드 렌더링, 포워드 렌더링이란? 그리고 차이점에 대해서 (0) | 2022.09.30 |
|---|---|
| 벡터의 내적(dot product) 한방에 이해하기 (1) | 2021.12.29 |
| UTF-8, 유니코드(UniCode)에 대하여 (0) | 2021.12.17 |
| [Unity] GameCenter로 Firebase인증하기 (1) | 2021.05.31 |
| [Unity] IOS Game Center 로그인하기 (매우 쉬움) (1) | 2021.05.31 |



댓글