벡터의 내적(dot product)
벡터의 내적이라 하면 흔히 두 벡터 간의 각도를 구하고 포워드 벡터를 이용해 앞면인지 뒷면인지 파악하는 정도로 간략하게 설명되어 있는 글이 대부분이다.
이와 같은 설명도 전부 맞는 말이지만 이는 벡터의 내적을 응용한 부분이고 내적이 의미하는 본질은 아니라고 생각한다.
그래서 내가 공부한 벡터 내적의 물리적인 본질을 서술해보겠다.
본래 벡터는 ‘위치, 힘, 방향’을 의미한다.
그리고 두 벡터를 내적한다 라는 말의 의미는 두 벡터가 작용한 일의 ‘효율’을 나타낸다.
어떤 물체에 힘을 가해서 움직이려 할 때
물체를 움직이려하는 방향(벡터) L (목표하는 방향)
물체에게 가한 힘의 방향(벡터) F
물체가 한 일의양 W
여기서 가해진 힘의 크기(F)가 원하는 방향(L)과 일치해서 작용한 힘의 양이 ‘유효한 일(W)’ 이 된다.

위 그림 같이 가한 힘(F)이 방향(L)과 100프로 일치하기에 힘이 100% 일로 작용을 한 것이고 효율은 100%라고 할 수 있다.
여기서 말하는 효율을 쉽게 말로 풀어보자면 F 와 L의 방향이 얼마만큼 일치하느냐를 의미한다.

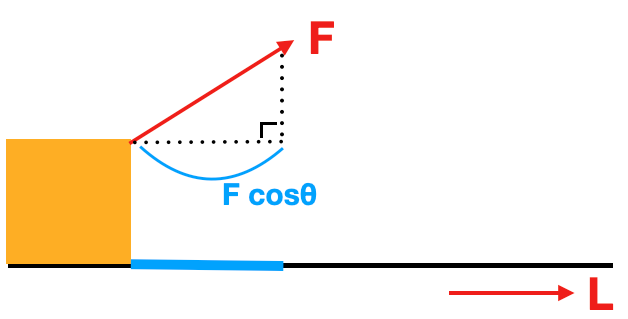
그럼 위 그림과 같이 힘(F)이 대각선으로 작용한 경우는 어떨까

F에서 L의 방향으로 작용하는 크기는 F cosθ 이다.
즉 여기서 유효한 힘의 크기는 F cosθ 이다.
물체가 한 일의 양 W를 구하는 식은 다음과 같이 나온다. F cosθ L
즉 벡터의 내적은 두 벡터의 작용의 효율성을 나타낼 때 사용된다.
단순히 F * L 의 곱셈은 두 벡터의 방향성을 제외시킨 그 벡터가 가지고 있는 스칼라끼리의 곱셈이 됨으로 두 벡터의 곱의 순수한 크기만을 의미하게 된다. 하지만 여기서 cosθ 을 곱하게 됨으로 F의 크기에서 L방향으로 작용하는 크기만을 추출하여 두 벡터의 ‘효율’을 의미하게 된다.
두 벡터가 수직인 경우
두 벡터가 수직으로 만나게 된다면 cosθ = 0 이 되고 두 벡터의 효율성은 0이 됨으로 내적 값 또한 0이 된다.

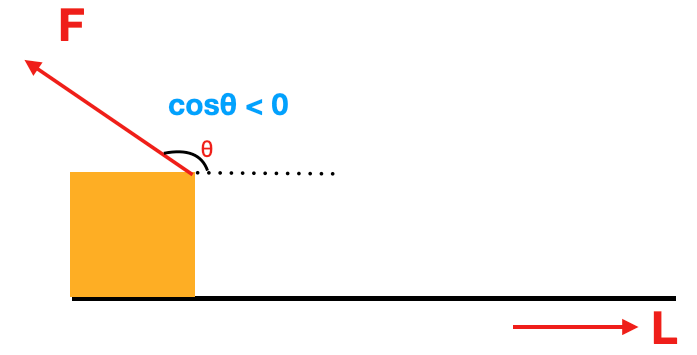
두 벡터의 각이 90도가 넘는 경우
두 벡터가 서로 다른 방향을 바라보는 경우(두 벡터의 각이 90도가 넘는 경우) 이 된다.
두 벡터 사이의 각도 구하기
를 통해 우리는 만큼의 각이 있을 때 밑변의 비율(x)을 구할 수 있다.
반대로 x의 값을 안다면 arccos(x)를 통해 를 구할 수 있다.
내적의 결과값은 두 벡터의 물리적인 작용 효율을 나타낸다고 설명했다.
그리고 이 두 벡터가 노말라이즈된 상태라면 이 효율은 두 벡터의 방향이 얼마만큼 일치하느냐를 나타내는 수치이다.
이 수치는 cos의 비율 값과 일치한다.
즉 노말라이즈 된 두 벡터 F, L 을 내적 한 결과값 x를 accos시키면 두 벡터가 이루는 각의 라디안 크기가 나온다. 이 라디안을 디그리 값으로 바꿔주면 두 벡터 사이의 각을 알 수 있다.
angle = arccos(Dot(F,L)) * 180/π
이러한 원리로 내적을 응용하여 몬스터를 공격할 때 플레이어가 뒤에 있는지 앞에 있는 지를 구분하여 백어택을 구현하는 것이며
시야 각안에 특정 물체가 있는지, 렌더링 시 라이팅 벡터와 폴리곤의 노말을 내적 하여 라이팅 처리를 하는 등 수많은 부분에서 응용이 되고 있다.
https://hub1234.tistory.com/46
[게임수학]라디안(호도법)이 뭐라고 ?
Radian 라디안(호도법)이란? 라디안이라는 것은 각도를 수치로 나타내기 위해 나타난 개념임. 그런데 라디안을 왜 쓰냐고 ? 삼각함수의 수학적 응용을 늘리고, 삼각함수에 대한 계산을 편하게 하
hub1234.tistory.com
https://hub1234.tistory.com/42
[게임수학]삼각함수 이해하기(sin, cos, tan)
해당 포스팅은 한 커뮤니티 싸이트에서 본 양질의 게시물을 좀 더 많은 사람에게 공유하기 위한 목적으로 재 업로드 합니다. 문제 발생 시 삭제하겠습니다. lab.gamecodi.com/board/zboard.php?id=GAMECODILAB_
hub1234.tistory.com
'개발이야기' 카테고리의 다른 글
| 순열(Permutation)과 조합(Combination)에 대해 이해하기 (0) | 2022.10.27 |
|---|---|
| 디퍼드 렌더링, 포워드 렌더링이란? 그리고 차이점에 대해서 (0) | 2022.09.30 |
| [게임수학]라디안(호도법)이 뭐라고 ? (0) | 2021.12.25 |
| UTF-8, 유니코드(UniCode)에 대하여 (0) | 2021.12.17 |
| [Unity] GameCenter로 Firebase인증하기 (1) | 2021.05.31 |



댓글