삼각함수 이해하기(sin, cos, tan)
해당 포스팅은 한 커뮤니티 싸이트에서 본 양질의 게시물을 좀 더 많은 사람에게 공유하기 위한 목적으로 재 업로드 합니다.
문제 발생 시 삭제하겠습니다.
탄젠트(tan)
나무가 너무 높아서 직접 올라가서 잴 수 없으니 태양의 고도가 45도 일 때 나무의 그림자 길이를 재서 나무의 높이를 알아냈다고 한다.
그림처럼,,

위 그림을 보면 두 변의 길이가 같은 이등변 삼각형이 나온다는 것을 알 수 있다.
이등변 삼각형은 두 변의 길이가 같으니 나무의 그림자의 길이는 곧 나무의 높이와 같다는 사실 또한 알 수 있다.
그리고 이 삼각형은 직각 삼각형이라는 것은 말안해도 알 수 있을 것이다.
그리고 이 내용이 삼각함수 탄젠트의 대한 내용이다.

탄젠트 45도를 계산해보면 1이라는 결과값이 나온다.
이 결과값은 비율을 나타낸 것인데 어떠한 비율이 1이라는 것은 비교 대상이 서로 똑같다 라는 뜻이다.
각도가 45도 일 때 그림자의 길이와 나무의 높이를 비교해 봤더니 둘이 똑같더라,
즉,

이것을 좀 더 삼각함수스럽게 표현하면 이렇게 쓴다.
tan(45°) = 1tan은 삼각함수중 하나인 탄젠트라는 함수인데 지각 삼각형에서 어떠한 각도를 넣었을 때 밑변과 먼변(수직인 변)의 비율을 구해준다.
위 예제에서 그림자의 길이와 나무의 높이의 비율을 구했던 것처럼
사인(sin)
이번에는 눈썰매장을 만든다고 해보자.
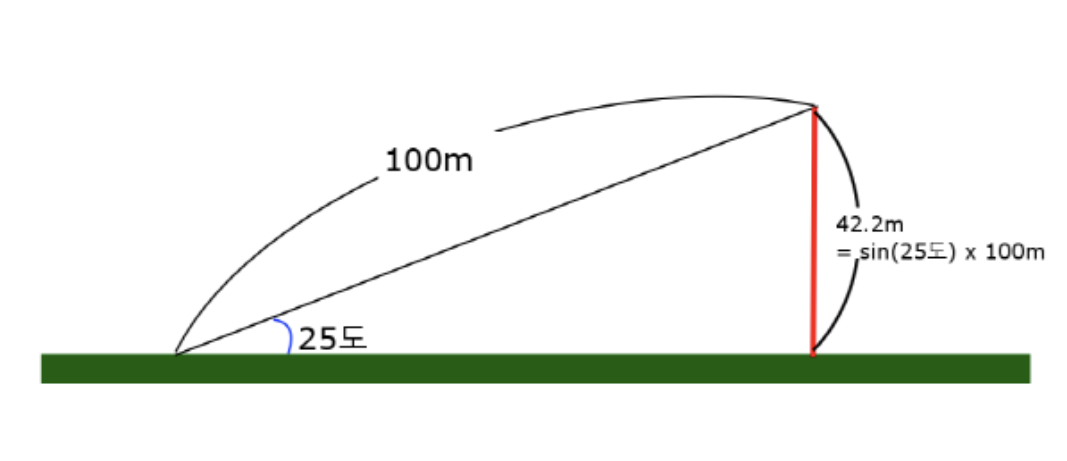
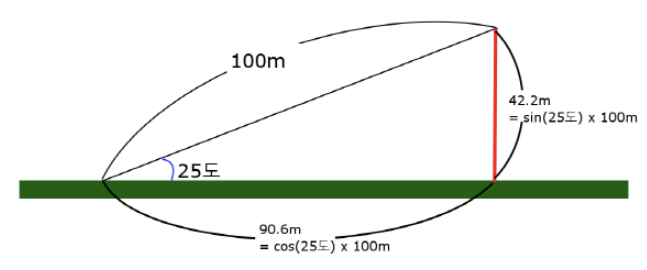
25도 각도 경사에다가 100미터 짜리 슬로프를 만든다고 해보자
그림으로 그리면 이런 모습일 것이다.

그런데 슬로프의 길이와 각도는 정했는데 기둥의 높이를 몇 미터로 해야 되는지 모른다는 것이다.
그런데 그림을 보니 이번에도 직각 삼각형이다.
이러면 삼각함수를 써서 알아낼 수 있다.
다만 밑변의 길이나 높이는 모르니 탄젠트는 쓸 수 없다.
sin은 제일 긴 빗변과 높이의 비율을 구해주는 함수이다.
위 그림에서는 100m짜리 슬로프가 빗변을 의미 하는데 sin함수를 통해서 빗변과 먼변(높이)의 비율을 구한 뒤 빗변의 길이만큼 곱해주면 높이 값이 나오게 된다.

계산기로 sin(25)를 계산한 결과

sin(25°)에 빗변의 길이인 100을 곱해준 결과
이렇게 해서 기둥의 높이는 42.2... 미터가 된다.
자 여기서,
직각 삼각형에서 한 각도를 선택해 sin(25°)를 계산한 것 까지는 알겠는데, 왜 이 결과값에 슬로프의 길이인 100을 곱해서 높이를 구한 것 일까?
sin은 빗변과 높이의 ' 비율 ' 을 구해주는 함수이기 때문이다.

sin(25도) = 0.422 라는 것은 슬로프의 길이(빗변)에 비해 기둥의 높이(먼변)가 0.422배 작다 라고 생각할 수 있다. 따라서 슬로프의 길이가 100m 라면 기둥의 높이는 100m에 비해 0.422배 작기 때문에
100 x 0.422 = 42.2 가 되는 것.
코사인(cos)
sin함수는 기둥의 높이를 잴 때 사용했다.
코사인(cos)함수는 밑바닥의 길이를 잴 때 사용할 수 있다.
눈썰매장을 다시 보자.
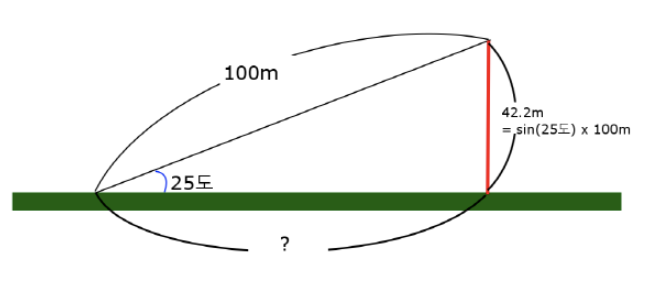
피타고라스의 정리를 사용해도 바닥의 길이를 구할 수 있지만, 삼각함수 cos를 사용해보자.
코사인(cos)함수는 빗변과 밑변(바닥)의 비율을 계산해 주는 함수이다.
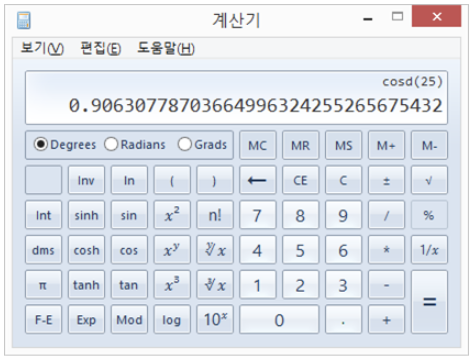
코사인(25도)의 결과값
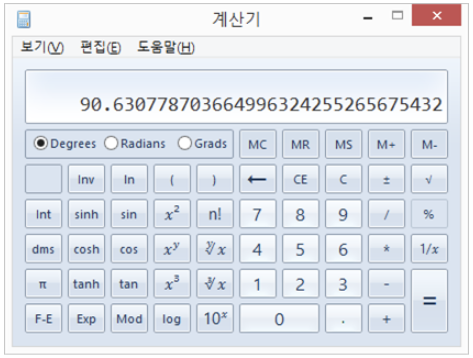
이 값에 슬로프의 길이인 100을 곱하면...
삼각함수 정리
사인(sin) = 빗변과 먼변(높이)의 비율을 구한다.
코사인(cos) = 빗변과 밑변의 비율을 구한다.
탄젠트(tan) = 밑변과 먼변(높이)의 비율을 구한다.
삼각함수는 직각 삼각형에 대해서 하나의 각이 주어졌을 때 각 변에 대한 비율을 구해준다.
https://hub1234.tistory.com/48
[게임수학]벡터의 내적(dot product) 한방에 이해하기
벡터의 내적(dot product) 벡터의 내적이라 하면 흔히 두 벡터 간의 각도를 구하고 포워드 벡터를 이용해 앞면인지 뒷면인지 파악하는 정도로 간략하게 설명되어 있는 글이 대부분이다. 이와 같은
hub1234.tistory.com
https://hub1234.tistory.com/46
[게임수학]라디안(호도법)이 뭐라고 ?
Radian 라디안(호도법)이란? 라디안이라는 것은 각도를 수치로 나타내기 위해 나타난 개념임. 그런데 라디안을 왜 쓰냐고 ? 삼각함수의 수학적 응용을 늘리고, 삼각함수에 대한 계산을 편하게 하
hub1234.tistory.com